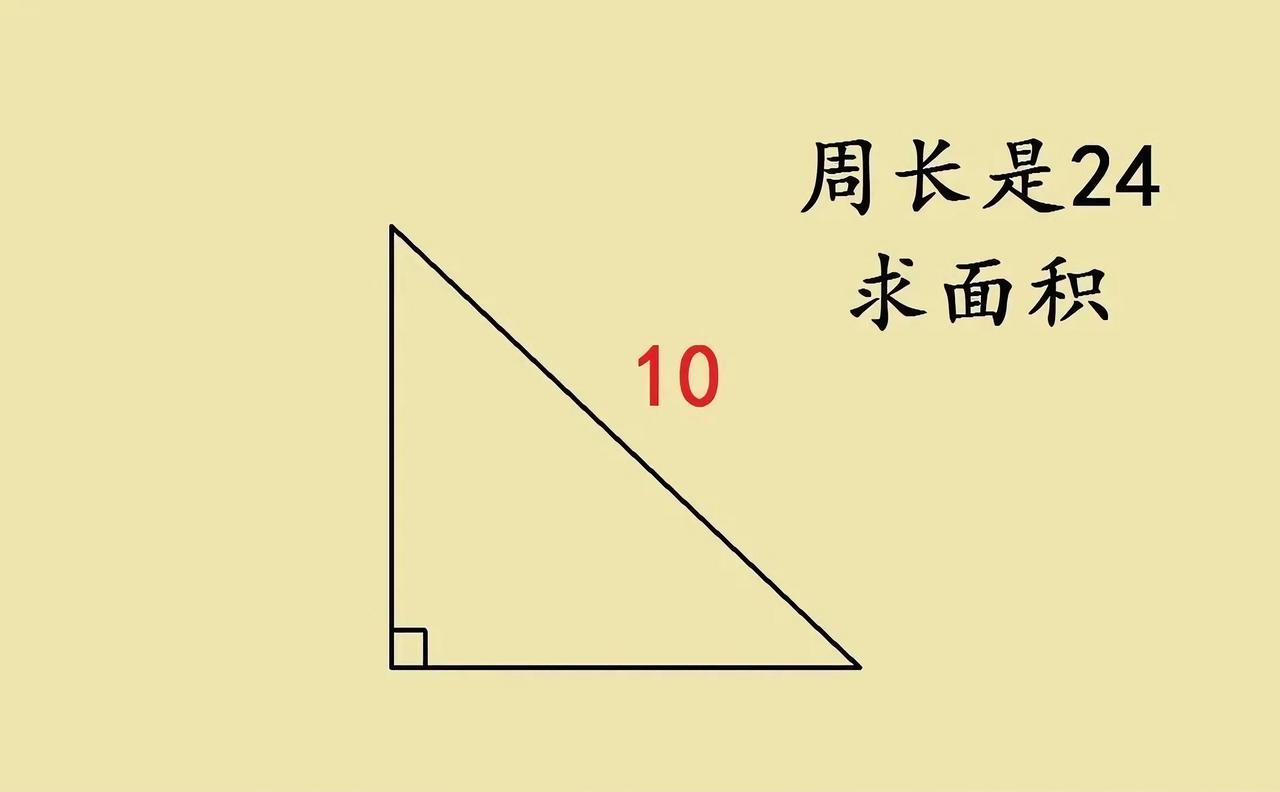
有位家长朋友发来这道小学六年级数学竞赛题,并表示非使用勾股定理、三角形相似不可,而且还要求解一元二次方程,可这全都是初中知识!他还说“自己想了半天、也没想出来不超纲的解题方法,只好向万能的友友们求助!”
如图

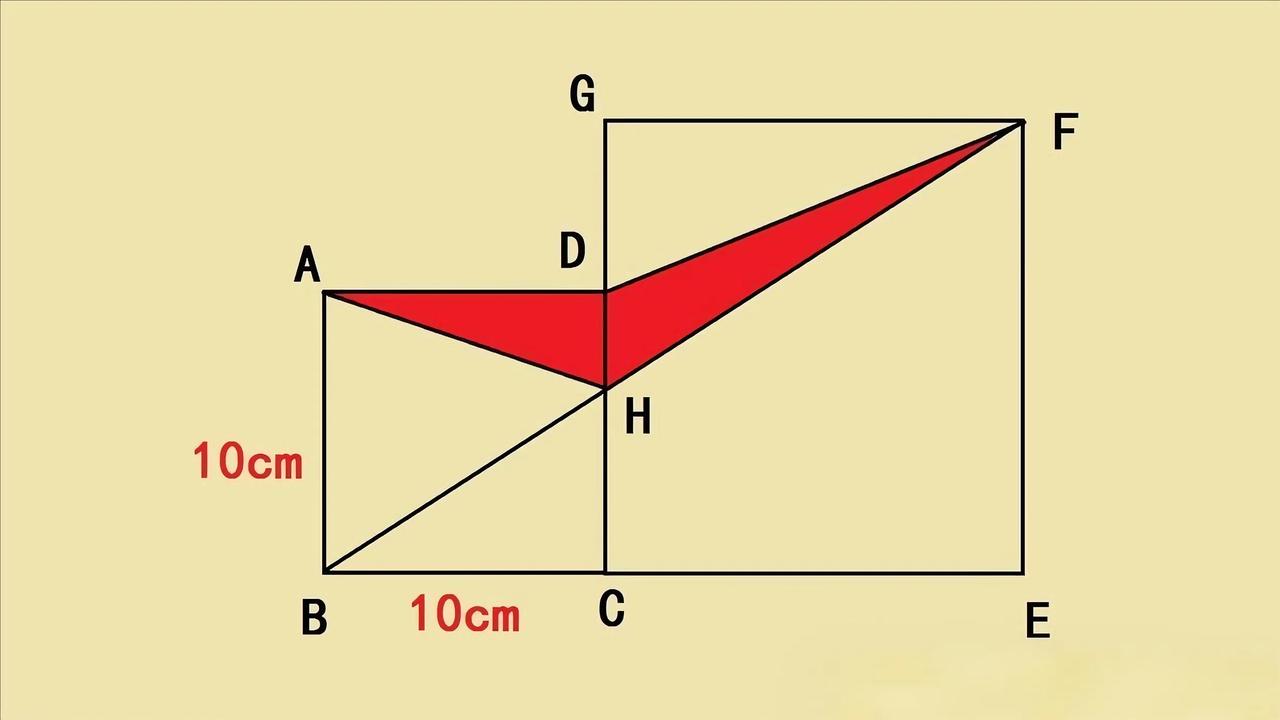
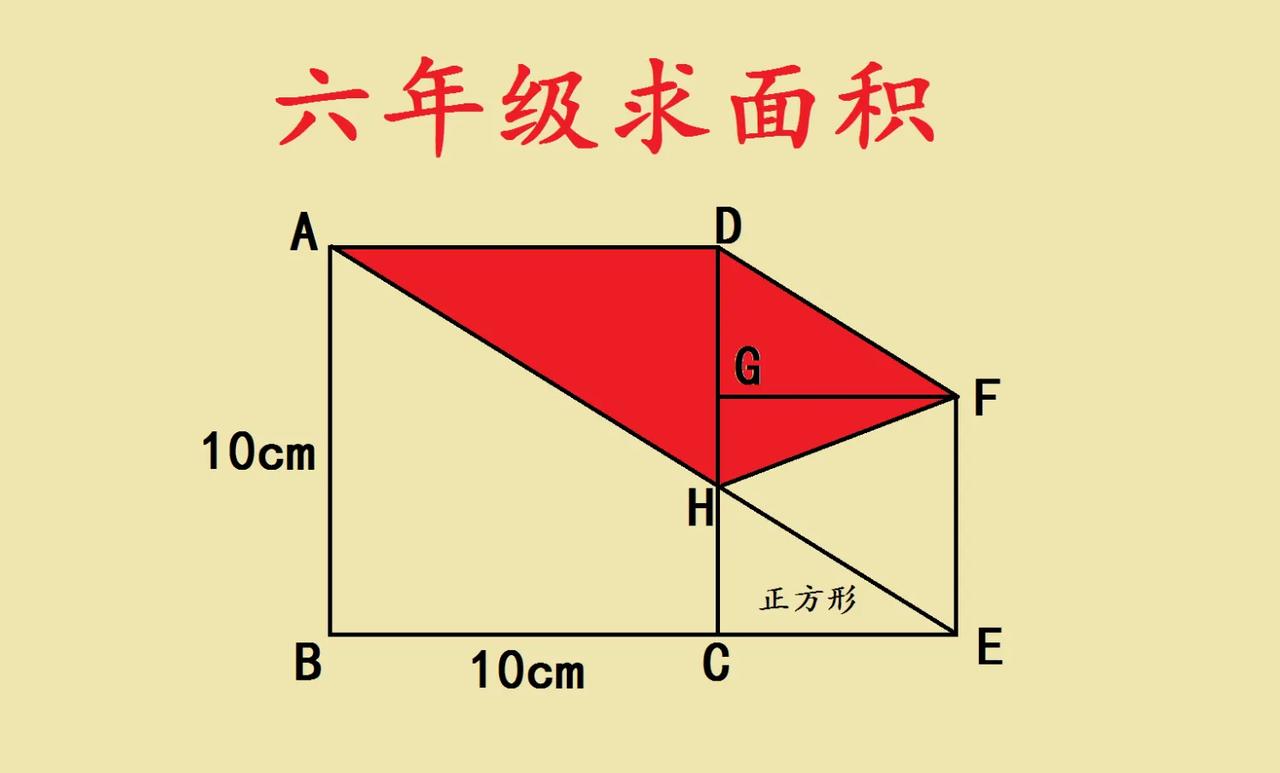
三个正方形如图放置,ABC为直角三角形,蓝色和黄色正方形面积分别为45和4,求红色正方形面积。
————————————————
这家长提供的超纲解答思路:勾股定理+三角形相似(平行线段比)+求解一元二次方程!
①令AB=a,BC=b,由勾股定理可得a²+b²=45。
②由△ADE∽△ABC(或DE⫽BC)可得AD/AB=DE/BC即ab=2(a+b)。
③由①和②可得(a+b)²=a²+b²+2ab=45+4(a+b),求得a+b=9或-5(舍弃)。
④由②和③可得ab=18,因此a=6,b=3。
尝试尽量不使用超纲知识作答,也以失败告终,必须求解一元二次方程!
①规避勾股定理(相当于证明勾股定理或平方和公式):将△ABC绕点A逆时针旋转90°至AB与AF重合,并据此以AC为弦作外弦图可知:蓝色正方形可由4个与△ABC的相同的三角形拼成,中间空白部分为1个以AB-BC为边长的小正方形,仍记AB=a,BC=b,则有45=4S△ABC+S小正方形即45=2ab+(a-b)²。
②规避三角形相似:连接BE,则ab/2=S△ABC=S△ABE+S△BCE=a×DE÷2+b×BD÷2=(a+b)×DE÷2=a+b即ab=2(a+b)。
③但求解a、b时,必须求解一元二次方程!
—————————————————
友友们,怎么看?欢迎留言分享!


评论列表