[LG]《Who Said Neural Networks Aren't Linear?》N Berman, A Hallak, A Shocher [Ben-Gurion University & NVIDIA & Technion] (2025)
线性化神经网络新突破:Linearizer框架全解析
神经网络被广泛认为是非线性的,但线性其实是相对于特定向量空间的。最新论文《WHO SAID NEURAL NETWORKS AREN’T LINEAR?》提出Linearizer架构,通过在两个可逆神经网络之间夹入一个线性算子,实现了在新定义的向量空间中将传统非线性网络变为精确线性映射!
核心思想:
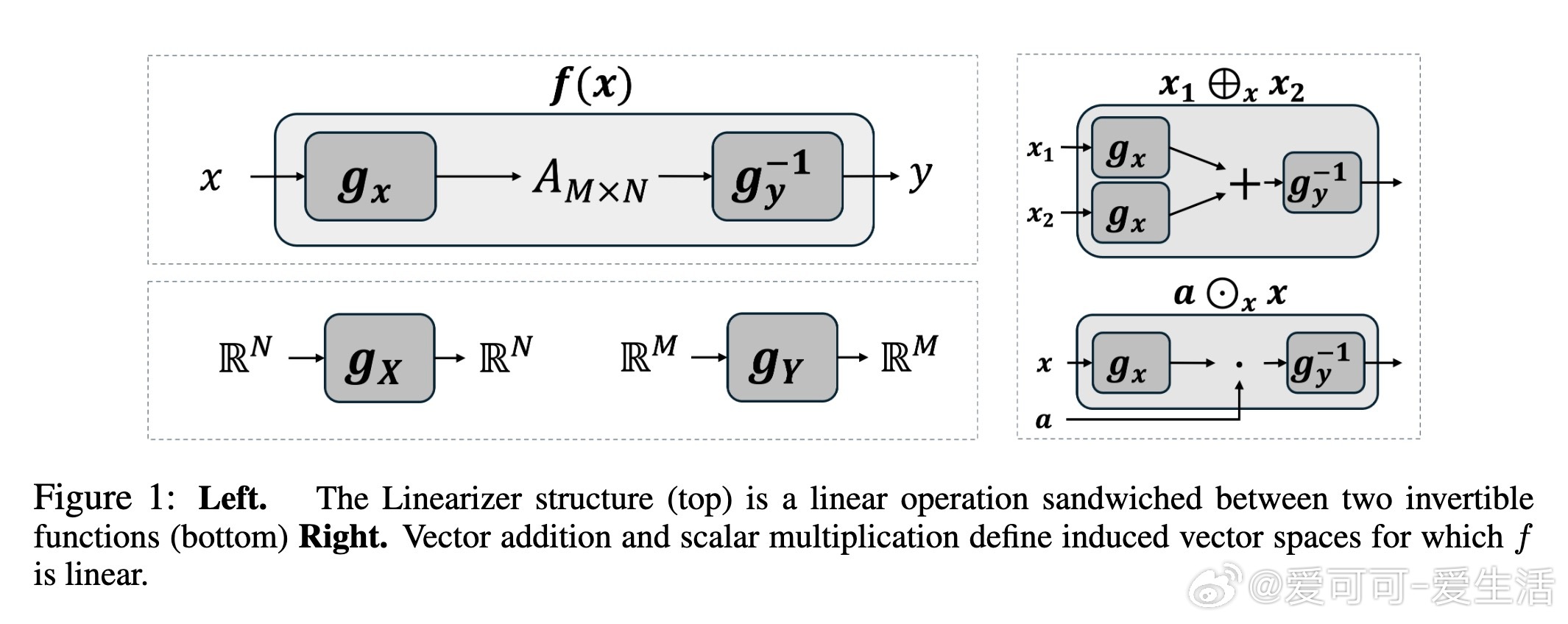
1️⃣ 利用两个可逆网络gx和gy定义加法和数乘的新操作,从而诱导出新的向量空间X和Y。
2️⃣ 在这两个空间间,夹入一个线性算子A,使得整个映射f(x) = g_y⁻¹(A g_x(x))是线性的。
3️⃣ 线性算子A的性质直接映射到f,支持奇异值分解、伪逆、正交投影等线性代数工具。
4️⃣ 线性映射的复合仍为Linearizer,支持多种组合操作。
三大应用亮点:
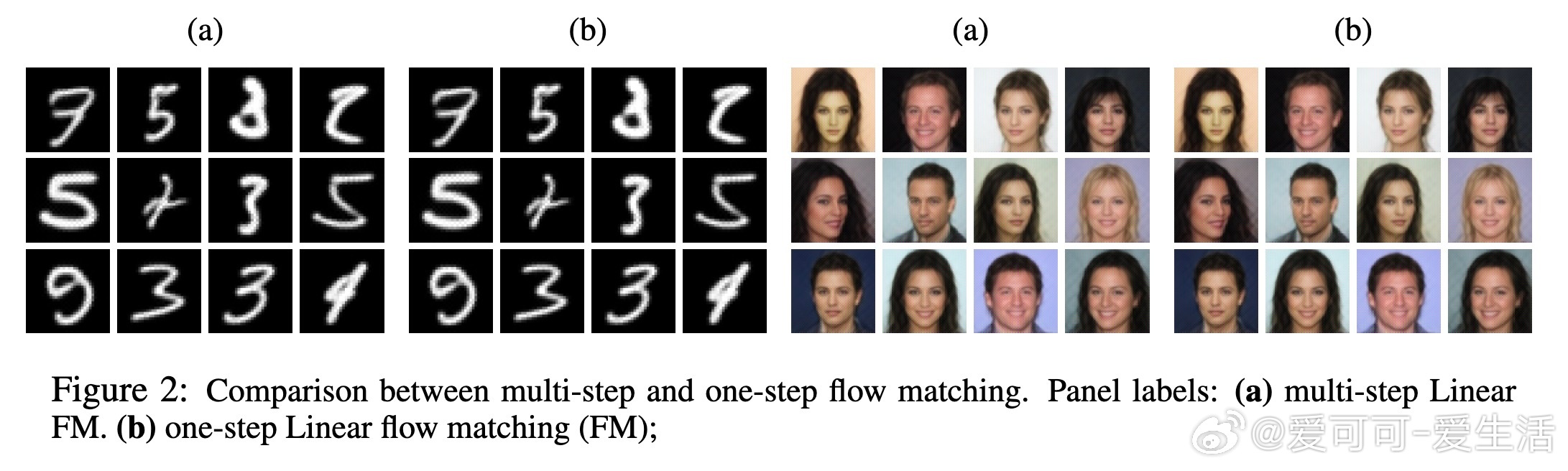
🔹 一步流匹配(One-step Flow Matching):传统扩散模型需要多步采样,我们通过Linearizer只需一步即可完成生成,极大提升效率且效果相当。
🔹 模块化风格迁移:将风格映射为线性算子,风格间线性插值实现自然过渡,风格组合更加灵活。
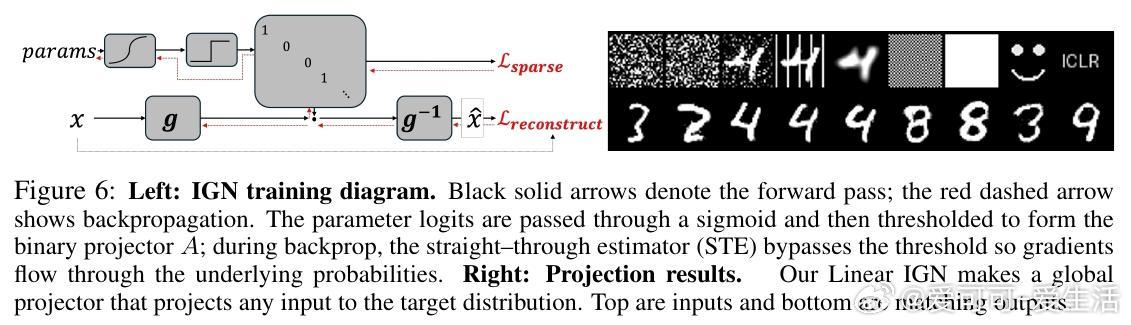
🔹 架构级幂等性实现:通过设计线性幂等算子,实现全局投影生成模型,解决传统幂等性训练难题。
理论贡献:
- 定义新向量空间的加法与数乘操作,证明其完备性与Hilbert空间结构。
- 证明Linearizer映射的伪逆也为Linearizer,支持精确编码与解码。
- 提供线性算子A的奇异值分解对应整体网络的SVD,实现线性代数分析工具的无缝迁移。
实验验证:
- MNIST与CelebA数据集上的一步流匹配生成质量与传统多步采样等效,FID分数接近且采样速度显著提升。
- 通过线性伪逆实现高质量图像插值与逆映射,验证信息保真性。
- 风格迁移示例展示多种风格的自然过渡与融合,支持模块化风格组合。
- 幂等生成模型实现任意输入的投影,输出匹配目标分布,展现全局投影潜力。
未来展望:
- 扩展Linearizer至更大规模与高分辨率数据,推动高效生成模型发展。
- 利用线性算子矩阵指数模拟连续时间动态,开辟物理与时序建模新途径。
- 深入理论分析Linearizer的表达能力极限,结合其他算子学习框架拓展应用。
论文链接:arxiv.org/abs/2510.08570
Linearizer架构突破了神经网络非线性的传统认知,架起了非线性表达力与线性代数解析力之间的桥梁,开启了神经网络设计和应用的新纪元。值得机器学习研究者和实践者深入关注!
神经网络 线性代数 生成模型 扩散模型 风格迁移 机器学习 AI研究