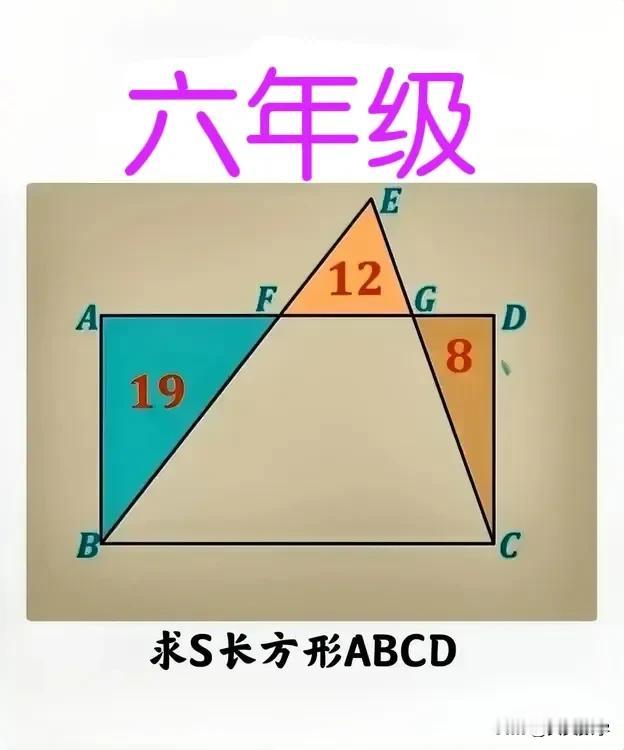
“会者口算,难者白卷!”这是一道某校“小升初”测试附加题:长方形局部面积已知,求其整体面积! 如图,E为长方形ABCD外一点,连接BE和CE,分别与AD相交于点F和点G,三角形AEF、EFG和CDG的面积分别为19、12和8,求长方形ABCD的面积。 ————————— 提示:将△CDG向左平移至CD与AB重合,平移后的三角形记为ABG',连接BG和EG'。 ①显然,S△BFG'=19+8=27,S△BFG=S△EFG'。 ②由等高三角形面积比等于底边之比可得, S△EFG'/S△BFG'=EF/BF=S△EFG/S△BFG,从而S△BFG×S△BFG=27×12,故S△BFG=18。 ③S长方形ABCD=2×(S△ABF+S△BFG+S△CDG)。 友友们,怎么看?欢迎留言分享! #小学数学# #妙笔生花创作挑战#
评论列表