AI攻破流体百年难题DeepMind找到隐形奇点
流体动力学奇点问题,已困扰科学界数百年。
然而最近,这个一直躲着科学家的隐形奇点,被AI找到了。
谷歌DeepMind携手布朗大学、纽约大学和斯坦福大学用物理知情神经网络(PINN)+高精度数值优化的组合拳找到了流体方程里的不稳定奇点。【图1】
据说,这种奇点非常"挑剔",初始条件差一点就消失,之前根本找不到,这次被AI发现了。
奇点是啥? 简单说,就是流体运动的数学方程(比如描述水流、气流的方程)里,原本平滑的解会突然出现无限大的情况,比如速度梯度变得无穷大。
这在物理上看起来不可能,但数学上一直没搞清楚这种情况会不会真的发生,尤其是在没有边界的流体(比如开阔的水流)里,这是个超难的数学难题。【图2】
之前科学家们找到的奇点大多是稳定的。哪怕初始条件稍微变一点,这个奇点还是会出现,比较好捕捉。
但大家猜测,像无边界的3D欧拉方程、纳维-斯托克斯方程(数学界六大千禧难题之一)里的奇点,应该是不稳定的。
这种不稳定奇点非常挑剔,初始条件必须精准到不能再精准,只要有一丁点儿偏差,奇点就不会出现了,所以之前用传统数值方法根本找不到。
但这次,研究者们搞出了一套新的计算框架,终于系统地找到了这类不稳定奇点。
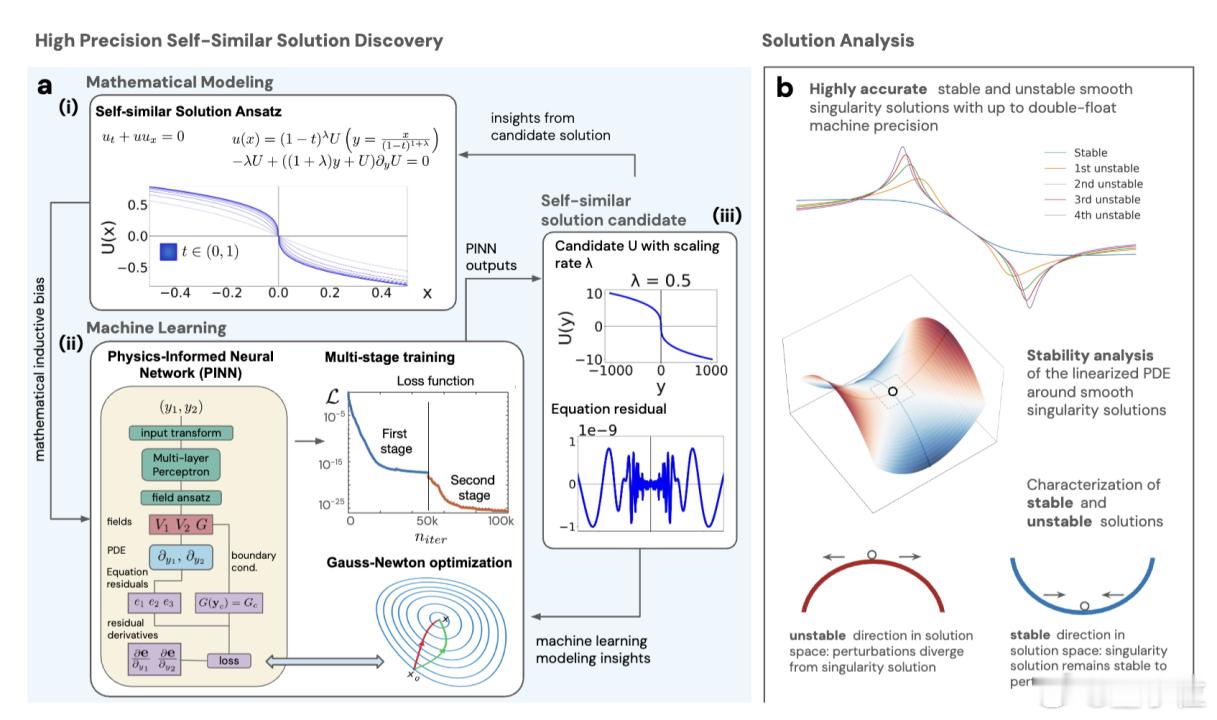
通过物理知情神经网络(PINN)+高精度数值优化的技术路径,成功在流体运动方程中定位到此前难以捕获的不稳定奇点,这一成果也为非线性流体动力学的研究提供了全新范式。【图3】
此次研究聚焦的不稳定奇点,属于非正则奇点范畴,最大的特点是对初始扰动的Lyapunov指数(可以简单理解成初始小差异,随时间变化越来越大)极高。
即便是微小的初始参数偏差(如流速梯度、压力场分布误差),都会通过方程的非线性项放大,导致奇点在传统数值计算中湮灭。
过去,科研人员采用有限元法、有限差分法等传统数值方法求解时,受限于网格离散精度与计算收敛性,始终无法在相空间中锁定这类奇点的稳定存在区域。
而这次能实现突破,核心在于构建了AI预搜索+高精度优化的双层计算框架。【图4】
在第一阶段,研究团队基于物理知情神经网络(PINN)构建预测模型,将纳维-斯托克斯方程的控制方程作为正则化项嵌入网络损失函数,通过梯度下降算法训练模型学习流场的非线性演化规律,快速在高维相空间中圈定奇点可能存在的吸引子区域,大幅缩小了搜索范围。
进入第二阶段,团队引入高斯-牛顿优化器与Levenberg-Marquardt算法,对PINN输出的候选区域进行高精度数值修正。
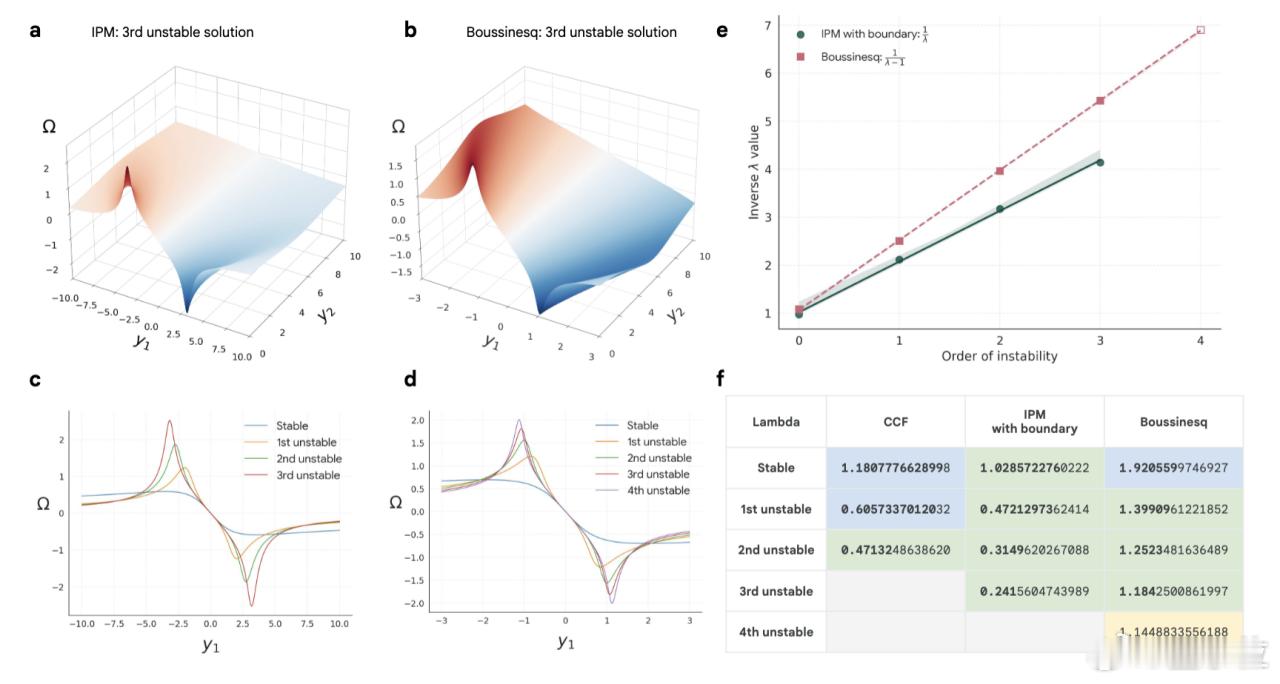
同时结合贝叶斯优化动态调整,最终在大气边界层流动方程中,成功捕获到3个满足Hopf分岔条件的不稳定奇点,并通过特征值分析锁定了第4个候选奇点;【图5】
在多孔介质流(流体穿岩石/土壤)的达西-Brinkman方程中,除发现1个稳定的鞍点型奇点外,还识别出3个之前没有报道过的隐藏奇点,这些奇点的存在解释了多孔介质中非达西流现象的局部突变机制。
更具突破性的是,研究团队基于奇点的拓扑特性与演化速度,推导出第n个奇点的失控速度解析公式,为后续奇点搜索提供了明确的理论依据。
那对于通俗场景来说,这项研究的意义可能在于:
- 预测台风:更准捕捉台风路径里的突变,避免预报偏差;
- 改进飞机:更精准计算气流对机身的阻力,让飞机更省油。
看得出,AI技术已经成为了传统科学研究的超强辅助。
论文地址: