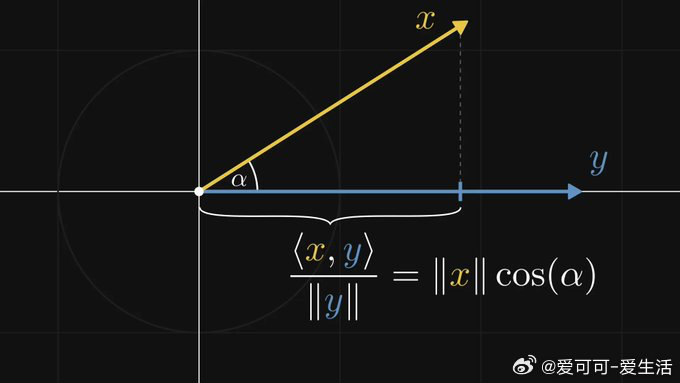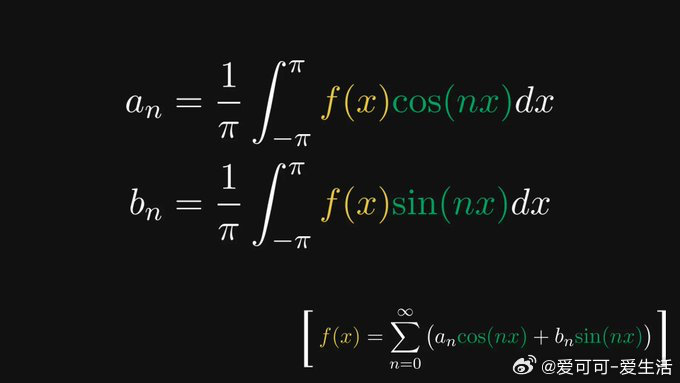傅里叶级数和笛卡尔坐标系有什么共同点?其实它们几乎是同一个概念的两种表现形式。
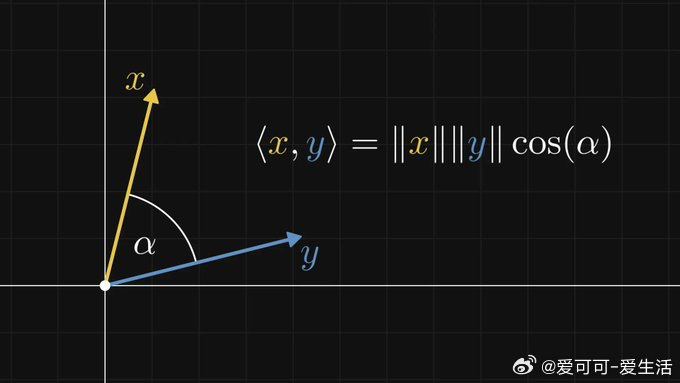
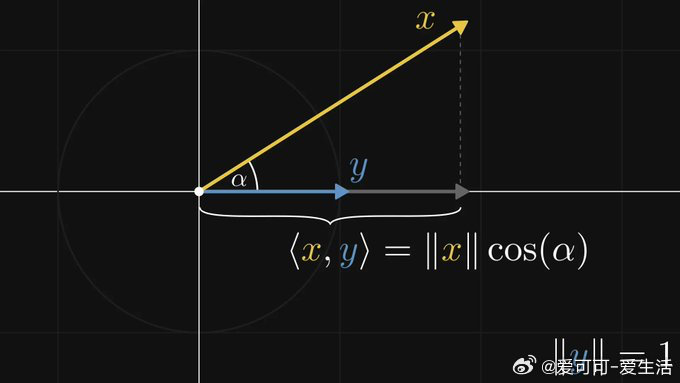
核心在“内积”:在欧几里得平面,内积对应“模长×模长×夹角余弦”,也就是向量投影的长度。如果第二个向量是单位向量,内积恰好是投影长度。
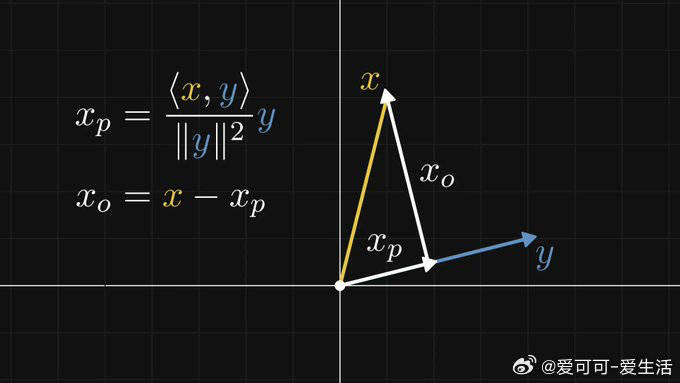
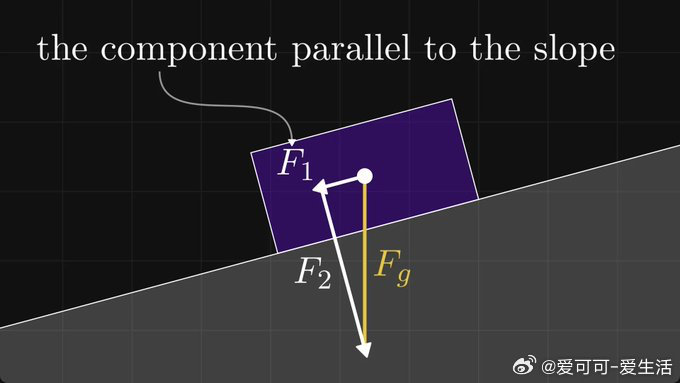
这让我们能用正交系统分解任意向量——比如物理中分析斜面滑动的力学问题。更重要的是,这一思想可推广到高维空间,产生了“标准正交基”:一组互相正交且单位长度的基向量。
为什么喜欢正交基?因为用内积就能直接求出向量在基上的坐标,无需解线性方程,极大简化计算。
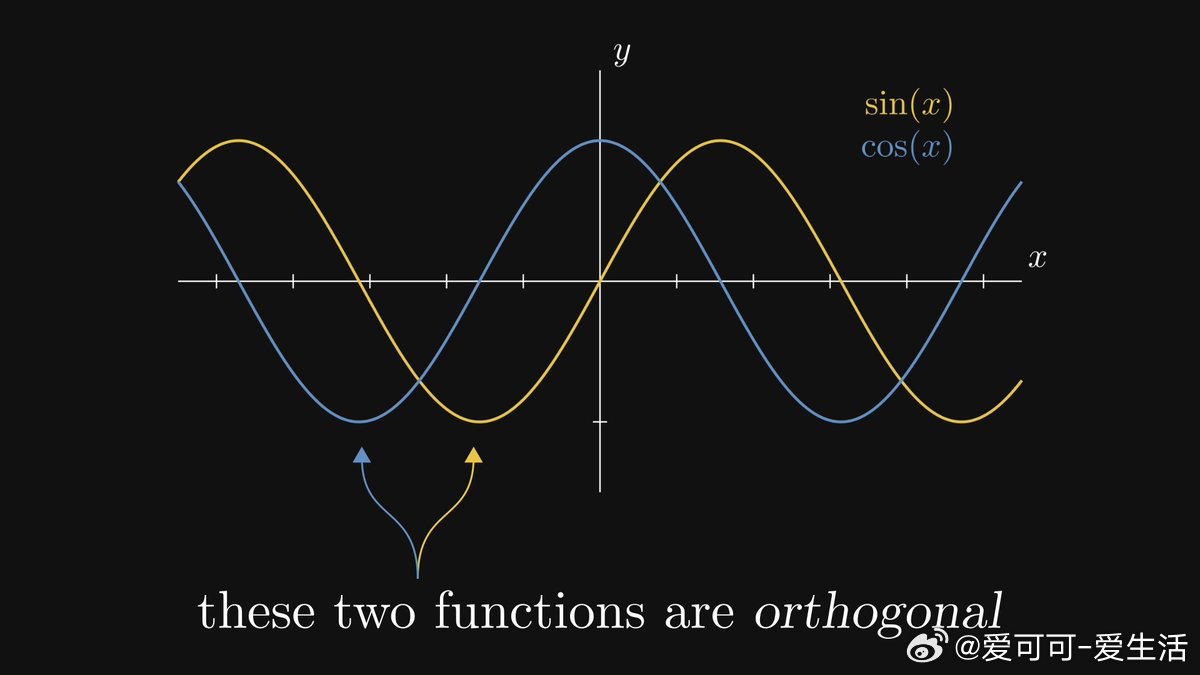
傅里叶级数正是基于正交基的思想。正弦和余弦函数(及其频率调制版本)构成L²空间的标准正交基,任何周期函数都能表示为它们的线性组合。
虽然技术细节复杂(如等式是L²意义上的收敛而非逐点收敛),但对于光滑函数,傅里叶展开是无懈可击的。
在L²空间,内积由积分定义,因此傅里叶系数能方便地通过积分计算。
这背后的数学不仅美妙,还与机器学习密切相关。掌握代数、微积分和概率,理解内积与正交基是构建复杂模型的基石。
——
原推文链接:x.com/TivadarDanka/status/1973810232494284928
---
补充思考:
内积和正交基的概念贯穿线性代数、函数空间和信号处理,建立了从几何到分析的桥梁。理解这层联系,有助于更深刻地把握现代科学与工程中的核心工具,比如傅里叶分析、特征分解及神经网络的底层机制。