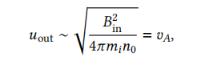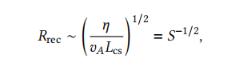磁性重连的定性以及磁性重连接的早期历史是怎样的? 第一次尝试处理我们今天通常称为“磁重新连接”的过程,一般归功于乔瓦内利(1947年)。他在1947年利用磁场线连接性的变化概念来解释太阳耀斑期间粒子的加速现象。 几年后,作为他的论文的一部分,詹姆斯·邓吉研究了电流层的性质,并展示了通过假设存在耗散过程可以改变连接性。Dungey是第一个提出“磁重新连接”这个名字的人。 随着对太阳耀斑的第一次观察,一些作者,尤其是Sweet和Parker,开发了一个简单的模型来解释稳态重新连接的工作原理。 为此,他们使用了将等离子体视为单一导电流体的模型,使用描述质量、动量和能量守恒的方程,以及描述磁场的感应方程。这组方程通常称为电阻磁流体力学(MHD)模型。在这个模型中,与我们使用的模型不同,等离子体受到粒子碰撞引起的电阻效应的扩散影响。 Sweet和Parker重新连接的基本配置如图片所示。这样一个二维的图像定性地展示了一个稳态重新连接区域的关键特征——一个具有垂直于平面的电流片、重新连接前后的磁场线(用红线和蓝线表示)、所谓的扩散区域(灰色区域)和中心处的中性点,称为X点(在此示意图中未显示),以及等离子体流动(绿色箭头)。 流动可以分为流入区(收敛于扩散区域)和流出区(指向远离扩散区域)。在此过程中,新重新连接的磁场在其自身张力下向外移动,加速流出的等离子体。 在二维的Sweet-Parker重新连接模型中,扩散区域是一个具有长度Lcs和宽度&cs的矩形区域。重新连接速率是指单位时间内重新连接的磁通量。作为一个初步的近似,这相当于计算重新连接区域上游和下游等离子体速度之比。 Sweet和Parker的分析方法是将质量连续性应用于二维的扩散区域,首先得到关系式,因此,重新连接速率可以用通常称为电流片纵横比的Acs = &cs/Lcs来进似计算。 现在我们考虑从电子动量守恒方程推导出的电阻欧姆定律,即E + v × B = j,其中j是电流密度,v是流体速度。在远离电流层的地方,电流密度很小,可以忽略电阻率。然而,在电流层内部,磁场线连接性的改变发生在磁场为零的点上。 此外,Sweet和Parker考虑了稳态重新连接过程,为了实现这样的过程,电场必须在整个区域上是均匀的。如果重新连接磁场的磁能几乎完全转化为流出等离子体的动能,那么能量守恒还要求将上游磁压与下游动压相等,这导致B2inuinLcs/4π ∼minOu3out&cs。这意味着对流速度的条件,其中vA是阿尔文速度。 以下是从Ji&Daughton(2011年)中提取的一些值:磁层边界和太阳冕:S ∼ 1 × 1013,太阳风:S ∼ 3 × 1012,Sgr A∗耀斑:S ∼ 5 × 1020。在等离子体实验中,S可能较小:ITER托卡马克:S ∼ 6 × 108。 因此,Sweet-Parker重新连接通常过慢,无法解释一些弱碰撞和无碰撞等离子体现象。典型的例子是太阳耀斑。仅仅考虑Sweet-Parker重新连接速率在太阳冕中提供的时间尺度(年)远远大于耀斑观测到的时间尺度(分钟)。 尽管Sweet-Parker模型存在局限性,扩散区域的特征在大多数重新连接问题中是共同的。 磁性重连作为一种重要的物理现象,在研究太阳风暴、地球磁层等领域都具有重要的应用价值,它的定性研究和早期历史发展为后续的研究提供了坚实的基础和理论依据。磁重联的理论研究不仅推动了磁重联机理的深入探究,还带来了许多重要应用,如磁约束聚变能量来源和许多其他融合实验中的应用,以及在空间探测和电磁加速器实验中的应用等。 尽管我们已经取得了许多重要的研究成果,但我们对于磁性重连的认知仍有很多未知和待探究之处。未来,我们需要持续投入精力和资源,不断深化对磁性重连的研究,探索和发现更多的磁重联现象,以期能产生更多的学术和应用价值,同时也帮助我们更好地理解宇宙万物的物理本质。